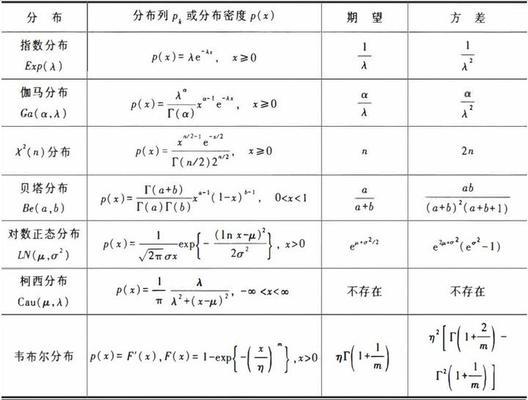
在概率论与统计学中,期望和方差是两个重要的概念,广泛应用于各个领域。本文将以期望与方差公式为主题,深入探讨它们的定义、计算方法和实际应用,帮助读者更好地理解和运用这两个概念。
文章目录:
1.期望与方差的基本定义和意义

-期望的定义及其在概率论中的意义
-方差的定义及其在统计学中的意义
2.期望与方差的计算方法

-离散随机变量的期望计算方法
-离散随机变量的方差计算方法
-连续随机变量的期望计算方法
-连续随机变量的方差计算方法
3.期望与方差的性质和公式推导
-期望的线性性质及其证明过程
-方差的性质及其证明过程
-期望与方差之间的关系及证明过程
4.期望与方差在统计分析中的应用
-期望与方差在样本调查中的意义和应用
-期望与方差在回归分析中的应用
-期望与方差在风险管理中的应用
5.期望与方差的误差分析与优化
-期望与方差的计算误差分析
-如何优化期望与方差的计算方法
-期望与方差优化在数值计算中的应用
6.期望与方差公式的扩展和变种
-高阶矩与累积量的定义和计算方法
-条件期望与条件方差的计算方法
-期望与方差公式在大数据分析中的改进
7.期望与方差在机器学习中的应用
-期望与方差在监督学习中的应用
-期望与方差在无监督学习中的应用
-期望与方差在强化学习中的应用
8.期望与方差公式的限制和局限性
-期望与方差公式的前提与限制条件
-期望与方差公式的局限性及其解决方法
9.期望与方差公式的历史与发展
-期望与方差概念的起源和发展历程
-期望与方差公式的数学推导历史
10.期望与方差在金融学中的应用
-期望与方差在资产定价模型中的应用
-期望与方差在投资组合优化中的应用
-期望与方差在衍生品定价中的应用
11.期望与方差的实例分析
-通过实例分析期望与方差的具体计算过程和应用场景
12.期望与方差公式的案例研究
-基于真实数据的期望与方差计算案例研究
-基于模拟数据的期望与方差计算案例研究
13.期望与方差在工程科学中的应用
-期望与方差在信号处理中的应用
-期望与方差在优化问题中的应用
-期望与方差在控制系统设计中的应用
14.期望与方差的扩展研究方向
-期望与方差在多维情况下的拓展研究
-期望与方差在非线性系统中的应用研究
-期望与方差在深度学习中的新方法研究
15.期望与方差公式的未来发展趋势
-期望与方差公式在大数据时代的发展趋势
-期望与方差公式在人工智能领域的新应用
期望与方差是概率论与统计学中的基础概念,对于数据分析、决策和风险管理至关重要。本文对期望与方差的定义、计算方法、性质、应用和未来发展进行了全面而深入的探讨,希望读者通过本文的学习,能够掌握期望与方差的核心概念和关键技巧,并能将其灵活应用于实际问题中。